Do?not?worry?about?your?difficulties?in?mathematics,?I?assure?you?that?mine?are?greater.
不要为你的数学难处担心,我保证我的更多.

1.基本概念与性质



补集,一般地,设U是一个集合,A是U的一个子集,由U中所有不属于A的元素组成的集合,叫做子集A在U中的
补集
。记作?UA。 
注意
:学习补集
的概念,首先要理解全集的相对性,补集符号?UA有三层含义:1、A是U的一个子集,即A?U;
2、?UA表示一个集合,且?UA?U;
3、?UA是由U中所有不属于A的元素组成的集合,?UA与A没有公共元素,U中的元素分布在这两个集合中。
这也是分类讨论的理论基础。

注:全集可以分成四小块每两者之间的交集是空集Φ,四个并在一起是全集U.
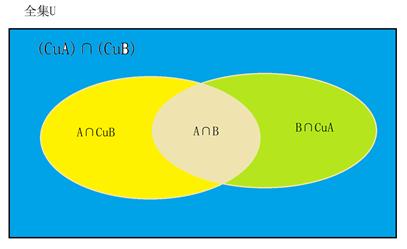
至此集合部分的基本内容已全部结束。
2.集合单元教学总结
集合是一个基础概念,即是一个是不能用其他概念加以定义的概念,也是不能被其他概念定义的概念。
应用广泛,现代数学各个分支的几乎所有成果都构筑在严格的集合理论之上。

它是一种思想、一种语言和一种工具,集合的知识已经渗透到自然科学的众多领域,集合的术语在科技文章和科普读物中比比皆是,帮助学生掌握好集合知识既是数学教学本身的需要,也是全面提高学生素质的一个必不可少的课题。但是,由于集合这一单元中,概念抽象,符号术语多,学习手段与方法跟学习初中数学有明显的差异,致使部分学生初学集合时,感到难以适应,常常因为概念理解上的偏差等原因而造成解题失误,进而影响对新知识的掌握。
一个人就好像一个分数,实际才能好比分子,而他对自己的估价好比分母。分母越大,则分数的值就越小。
要想学好集合,除了掌握集合的基本知识外,重点在“突出一种方法,渗透两种思想,掌握三种语言”三个方面下功夫。

一、突出一种方法——集合元素分析法
集合是一些对象的全体,其中的每一个对象叫做这个集合的元素。集合中的元素具有“四性”
1.确定性:集合中的元素应该是确定的,不能模棱两可。例如“个子高的学生的全体”、“漂亮的女生的全体”等都不能构成集合。
2.互异性:集合中的元素应该是互不相同的,相同的元素在集合中只能算作一个,只能写一次.例如不能有{1,1,2},而必须写为{1,2}.
3.无序性:集合中的元素间是无次序关系的.例如{1,2,3}与{3,2,1}表示同一个集合.
4.任意性:集合中的元素可以是任意的具体的确定的事物.例如数、式、点、形、物等
另外,集合的关系、集合的运算等等都是从元素的角度予以定义的.因此,求解集合问题时,抓住元素的特征进行分析,就相当于牵牛抓住了牛鼻子.
例1 已知,集合M,N如下,则M∩N等于 .

评注:注意集合M是求函数的值域,是个数集,而N是求函数的定义域,亦是个数集.只有弄清楚集合元素的特征,抓住代表元素代表的是谁,就可以有效的避免不必要的错误。

评注:本题中,利用集合元素的无序性和两集合相等时的元素特征,得出方程,例题的突破口在于元素0,利用互异性突破x,y.容易求得答案。变式亦利用上述方法打开了解题的大门分别求出值后,又利用元素的互异性进行检验,保证了所求结果的准确性,离开了元素分析法,必然寸步难行.
“如果用小圆代表你们学到的知识,用大圆代表我学到的知识,那么大圆的面积是多一点,但两圆之外的空白都是我们的无知面。圆越大其圆周接触的无知面就越多。” 芝诺
二、渗透两种数学思想——数形结合思想与分类讨论思想
布鲁纳说过,掌握数学思想可使得数学更容易理解和更容易记忆,领会数学思想是通向迁移大道的“光明之路”。集合单元中,含有丰富的数学思想内容,特别是数形结合的思想与分类讨论的思想,显得十分活跃,注意这些数学思想的挖掘、提炼和渗透,不仅可以帮助生有效地掌握集合知识的本质,驾驭集合问题的求解,而且对于开发学生的智力,培养学生的能力,优化学生的思维品质,具有十分重要的意义.

1.数形结合思想的渗透
集合与集合间的关系,集合中的交、并、补运算等问题,如果能以数形结合的思想为指导,借助图形进行思考,不仅可以使各集合之间的相互关系直观明了,而且也便于将各元素的归属确定下来,使抽象的集合运算建立在直观的形象思维基础之上,为问题的解决创设有益的情景.

评注:研究数集的相互关系时,可将题设通过数轴示意,借助直观性探求,即易于理解,又能提高解题速度。
例4 已知全集U={不大于15的正奇数},集合

求集合M,N.
分析:如下图,如小孩子看图说话一般容易。

评注:集合的韦恩图表示法,也具有直观形象的特点,它不仅能帮助我们深刻理解和记忆集合的概念、运算及其相互关系,而且能对一些较为复杂的涉及集合运算方面的问题提供一条简捷的解题途径。
练习:

2.分类讨论思想的渗透
分类的通俗说法是按照一定的标准把研究的对象分成几个部分或几种情况.它采取的是一种“化整为零、各个击破”的策略,通过这种策略可以达到将一个复杂的问题分解成若干个简单的问题,从而获得完整解答的目的.
例5

分析:
1、 讨论是如何产生的?方程最高次数项的系数是字母,注意从等于0开始讨论,本题即分为一次方程问题和二次方程问题。
2、 在二次方程问题中,方程的根有几种情况?符合本题意思有几种情况?交集是空集意味方程的根都是非正数吗?如果是如何求解?如果不是,又如何求解呢?
解略.
评注:分类讨论是一种重要的数学思想,在集合单元的教学中,注意分类讨论思想的渗透,帮助学生建立分类讨论的意识、掌握分类讨论的方法,不仅能够有效地提高学生解集合问题的能力,而且可以为以后进一步学习其他数学知识奠定坚实的基础.

3.补集思想的渗透
补集思想是补集的衍生物,故而在总结没有提到它,不过它一些题目中补集法还是相当重要的一种解题思想及考虑问题的方式,正难则反吗,有兴趣的可以想一想下面的问题如何解决.

三、掌握三种数学语言—一自然语言、符号语言、图形语言的转译
集合中的数学语言,其常见形式主要有三种:一是自然语言,通过日常语言来描述集合问题中的数学对象;二是符号语言,通过约定的数学符号来表述集合问题中的数学对象;三是图形语言,通过图形来表示集合问题中的数学对象.
本文中对集合的交、并运算概念的阐述均使用了三种语言形式,注意体会。
例6.

评析:你读懂了前面一个集合指的是什么吗?这是个点集,它指的是函数图像上所有的点。后面一个集合哪?它指的是直线x=1上的点。考察的是函数的定义,函数的图像与纵坐标轴或与其平行的直线最多有一个交点。
例7.看个书上的原题吧!别说书上的题目都简单。

评注:可借助函数的圈图来解决比较简单。因为值平方等于4,1的有+2,-2,+1,-1四个,保证值域中有4,1.所以上面四个数的选择方法有两个元素的有4个,三个元素的有4个四个元素的有1个。既可以分类讨论,也可以画图解答。
Imagination?is?more?important?than?knowledge. 想象力比知识重要.
例8.

分析:集合A表示的是直线上去掉一点之后的图形,集合B表示的是整条直线。如下图可的答案{}。

评析:关于点集的问题,常常将其转化为直角坐标平面上的图形的问题来加以研究,直观形象,简洁明了。例3的搭棚子的方法亦是数形结合的重点。

特别说明:本文以江苏版高中教材为蓝本.
